FAQ #

The FAQ for this lab can be found here.

Introduction #

The lab intro slides for this lab can be found here.

In this lab, you’ll create BSTMap, a BST-based implementation of the Map61B interface, which represents a basic tree-based map. You will be creating this completely from scratch, using the interface provided as your guide.

After you’ve completed your implementation, you’ll compare the performance of your implementation to a list-based Map implementation ULLMap as well as the built-in Java TreeMap class (which uses a BST variant known as a red-black tree).

Pulling from skeleton #

Follow the assignment workflow instructions to get the assignment and open it in IntelliJ. This assignment is lab07.

BSTMap #

In this lab (and future labs), we may not provide as much skeleton code as in the past. If you’re having trouble getting started, please come in to lab and/or use the resources linked below!

An algorithmic guide to put and get can be found here.

Create a class BSTMap that implements the Map61B interface using a BST (Binary Search Tree) as its core data structure. You must do this in a file named BSTMap.java! Your implementation is required to implement all of the methods specified in Map61B except for remove, iterator and keySet. For these methods you should throw an UnsupportedOperationException, unless completing the optional portion of the lab.

Your code will not compile until you create the BSTMap class and implement all the methods in Map61B. You can implement methods one at a time by writing the method signatures of all the required methods, but throwing UnsupportedOperationExceptions for the other implementations until you get around to actually writing them.

For debugging purposes, your BSTMap should also include an additional method printInOrder() (not given in the Map61B interface) that prints out your BSTMap in order of increasing Key. We will not test the result of this method, but you may find this helpful for testing your implementation!

In your implementation, you should ensure that generic keys K in BSTMap<K,V> implement Comparable. This is called a bounded type parameter.

The syntax is a little tricky, but we’ve given an example below. Here, we are creating a BSTSet for Comparable objects. We’ve included the rather strange compareRoots for pedagogical purposes (for a compareTo refresher, see this documentation):

public class BSTSet<K extends Comparable<K>> implements Set61B<K> {
    private class BSTNode {
        K item;
        // ...
    }

    private BSTNode root;

    /* Returns whether this BSTSet's root is greater than, equal to, or less
     * than the other BSTSet's root, following the usual `compareTo`
     * convention. */
    public int compareRoots(BSTSet other) {
        /* We are able to safely invoke `compareTo` on `n1.item` because we
         * know that `K` extends `Comparable<K>`, so `K` is a `Comparable`, and 
         *`Comparable`s must implement `compareTo`. */
        return this.root.item.compareTo(other.root.item);
    }

    // ...
}

IntelliJ has a nice feature that will generate the method signatures for you. If you’re implementing an interface and haven’t implemented all the methods, IntelliJ will highlight the class signature in red. If you hover over this, you should be able to select Implement methods. On the pop-up window, click “OK” with the default selections, and IntelliJ should populate the class with the required method signatures (they won’t be functional though!).

It should look something like this (you don’t have Set61B, this is just an example!):

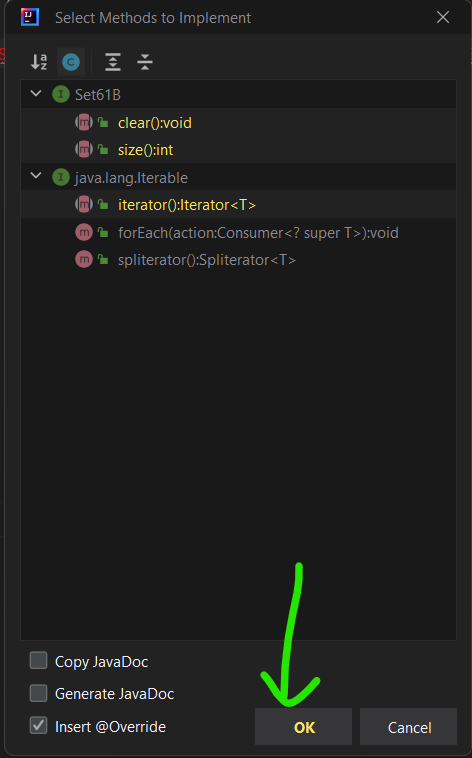
In this example, IntelliJ will generate the clear, size, and iterator method signatures, because that’s all our mythical Set61B interface requires. If you follow this procedure with your code, you should have all the method signatures required for Map61B. (You can also pick and choose which signatures to generate, if you’d like.)

Resources #

The following resources might prove useful:

• Lecture 16 slides.
• ULLMap.java (given in src/), an unordered, linked-list-based Map61B implementation.
• BST code from our optional textbook.

So… How Fast Is It? #

There are two interactive speed tests provided in InsertRandomSpeedTest.java and InsertInOrderSpeedTest.java. Do not attempt to run these tests before you’ve completed BSTMap. Once you’re ready, you can run the tests in IntelliJ.

The InsertRandomSpeedTest class performs tests on element-insertion speed of your BSTMap, ULLMap (provided), Java’s built-in TreeMap, and Java’s built-in HashMap (which you’ll explore more in the next lab). It works by asking the user for a desired length of each String to insert, and also for an input size (the number of insertions to perform). It then generates that many Strings of length as specified and inserts them into the maps as <String, Integer> pairs.

Try it out and see how your data structure scales with the number of insertions compared to the naive and industrial-strength implementations. Remember that asympototics aren’t representative on small samples, so make sure your inputs are sufficiently large if you are getting a confusing trend. Record your results in a file named speedTestResults.txt.

Now try running InsertInOrderSpeedTest, which behaves similarly to InsertRandomSpeedTest, except this time the Strings in <String, Integer> key-value pairs are inserted in lexicographically-increasing order. If you observed anything interesting, discuss it with your fellow students or a staff member!

Deliverables and Scoring #

The lab is out of 256 points. There is one hidden test on Gradescope (that checks your speedTestResults.txt). The rest of the tests are local. If you pass all the local tests and fill out the speedTestResults.txt file sufficiently, you will get full credit on Gradescope.

Submission #

Just as you did for the previous assignments, add, commit, then push your Lab 07 code to GitHub. Then, submit to Gradescope to test your code. If you need a refresher, check out the instructions in the Lab 1 spec and the Assignment Workflow Guide.

More (Ungraded) Exercises #

These will not be graded, but you can still receive feedback using the local tests (and on the autograder).

Implement the methods iterator(), keySet(), remove(K key) in your BSTMap class. When implementing the iterator method, you should return an iterator over the keys, in sorted order. remove() is fairly challenging - you’ll need to implement Hibbard deletion.

For remove, you should return null if the argument key does not exist in the BSTMap. Otherwise, delete the key-value pair (key, value) and return value.

Optional: Asymptotics Problems #

Check your answers against the solutions!

Given B, a BSTMap with N key-value pairs, and (K, V), a random key-value pair, answer the following questions.

Unless otherwise stated, “big-Oh” bounds (e.g. $\mathcal{O}(N)$) and “big-Theta” bounds (e.g. $\Theta(N)$) refer to the number of comparisons in the given method call(s).

For questions 1-7, state whether the statement is true or false. For question 8, give a runtime bound.

1. B.put(K, V) $\in \mathcal{O}(\log N)$
2. B.put(K, V) $\in \Theta(\log N)$
3. B.put(K, V) $\in \Theta(N)$
4. B.put(K, V) $\in \mathcal{O}(N)$
5. B.put(K, V) $\in \mathcal{O}(N^2)$

6. For a fixed key C not equal to K, both B.containsKey(C) and B.containsKey(K) run in $\Omega(\log N)$.
7. (This question is quite difficult.) Let b be a Node of a BSTMap, and two subtrees rooted at root, called left and right. Further, assume the method numberOfNodes(Node p) returns the number of nodes ($M$) of the subtree rooted at p and runs in $\Theta(M)$ time. What is the running time, in both the worst and best case, of mystery(b.root, z), assuming 1 <= z < numberOfNodes(b.root)?

Hint: See if you can work out what mystery does first, then see how it accomplishes it.

public Key mystery(Node b, int z) {
    int numLeft = numberOfNodes(b.left);
    if (numLeft == z - 1) {
        return b.key;
    } else if (numLeft > z) {
        return mystery(b.left, z);
    } else {
        return mystery(b.right, z - numLeft - 1);
    }
}